Simulating Random Populations

A short description of the post.

Author
Affiliation

Rodney Dyer

Center for Environmental Studies

Published

April 21, 2019

The gstudio package has routines that can be used to simulate random populations. I’ve added these to facilitate more exploratory data analysis. Here is how you can use them.

If you have not updated the gstudio and popgraph packages in a while, you probably should. Here is how (if it asks if you would like to update the other packages, it is probably a good idea to say yes).

devtools::install_github("dyerlab/popgraph")
devtools::install_github("dyerlab/gstudio")

Then load it in as:

library(gstudio)
Warning: replacing previous import 'dplyr::union' by 'raster::union' when
loading 'gstudio'
Warning: replacing previous import 'dplyr::intersect' by 'raster::intersect'
when loading 'gstudio'
Warning: replacing previous import 'dplyr::select' by 'raster::select' when
loading 'gstudio'

I’m going to start with the enigmatic bark beetle data set.

data(arapat)
summary(arapat)
      Species      Cluster      Population        ID         Latitude    
 Cape     : 75   CBP-C :150   32     : 19   101_10A:  1   Min.   :23.08  
 Mainland : 36   NBP-C : 84   75     : 11   101_1A :  1   1st Qu.:24.59  
 Peninsula:252   SBP-C : 18   Const  : 11   101_2A :  1   Median :26.25  
                 SCBP-A: 75   12     : 10   101_3A :  1   Mean   :26.25  
                 SON-B : 36   153    : 10   101_4A :  1   3rd Qu.:27.53  
                              157    : 10   101_5A :  1   Max.   :29.33  
                              (Other):292   (Other):357                  
   Longitude          LTRS          WNT            EN           EF     
 Min.   :-114.3   01:01 :147   03:03  :108   01:01  :225   01:01 :219  
 1st Qu.:-113.0   01:02 : 86   01:01  : 82   01:02  : 52   01:02 : 52  
 Median :-111.5   02:02 :130   01:03  : 77   02:02  : 38   02:02 : 90  
 Mean   :-111.7                02:02  : 62   03:03  : 22   NA's  :  2  
 3rd Qu.:-110.5                03:04  :  8   01:03  :  7               
 Max.   :-109.1                (Other): 15   (Other): 16               
                               NA's   : 11   NA's   :  3               
     ZMP           AML           ATPS          MP20    
 01:01 : 46   08:08  : 51   05:05  :155   05:07  : 64  
 01:02 : 51   07:07  : 42   03:03  : 69   07:07  : 53  
 02:02 :233   07:08  : 42   09:09  : 66   18:18  : 52  
 NA's  : 33   04:04  : 41   02:02  : 30   05:05  : 48  
              07:09  : 22   07:09  : 14   05:06  : 22  
              (Other):142   08:08  :  9   (Other):119  
              NA's   : 23   (Other): 20   NA's   :  5

To simulate random data sets we need to start off by determining what allele frequencies you may want. I’m going to use the stratum-level frequencies from the example data set. Here is what these look like.

suppressPackageStartupMessages( library(tidyverse) )
library(DT)
freqs <- frequencies(arapat, stratum="Population")
head(freqs)
  Stratum Locus Allele Frequency
1     101  LTRS     01 0.2777778
2     101  LTRS     02 0.7222222
3     101   WNT     01 1.0000000
4     101    EN     01 0.6111111
5     101    EN     03 0.3888889
6     101    EF     01 0.7142857

though the whole data set has 700 rows!

What I’m going to do is to create a random dataset from these frequencides. This dataset will have 20 populations (I’ll just grab the first 20 Stratum from this frequency matrix).

freqs %>%
  filter( Stratum %in% unique(freqs$Stratum)[1:20] ) -> sim_freqs
summary(sim_freqs)
   Stratum             Locus              Allele            Frequency     
 Length:370         Length:370         Length:370         Min.   :0.0500  
 Class :character   Class :character   Class :character   1st Qu.:0.1500  
 Mode  :character   Mode  :character   Mode  :character   Median :0.3500  
                                                          Mean   :0.4297  
                                                          3rd Qu.:0.7000  
                                                          Max.   :1.0000

And we can take a quick look at the frequencies across populations for, say MP20 as:

sim_freqs %>%
  filter( Locus == "MP20", Stratum %in% unique(Stratum)[1:5] ) %>% 
  ggplot( aes(Allele,Frequency)) + 
  geom_bar( stat="identity", position="dodge" )  + 
  facet_grid( Stratum ~ .) + 
  theme_bw()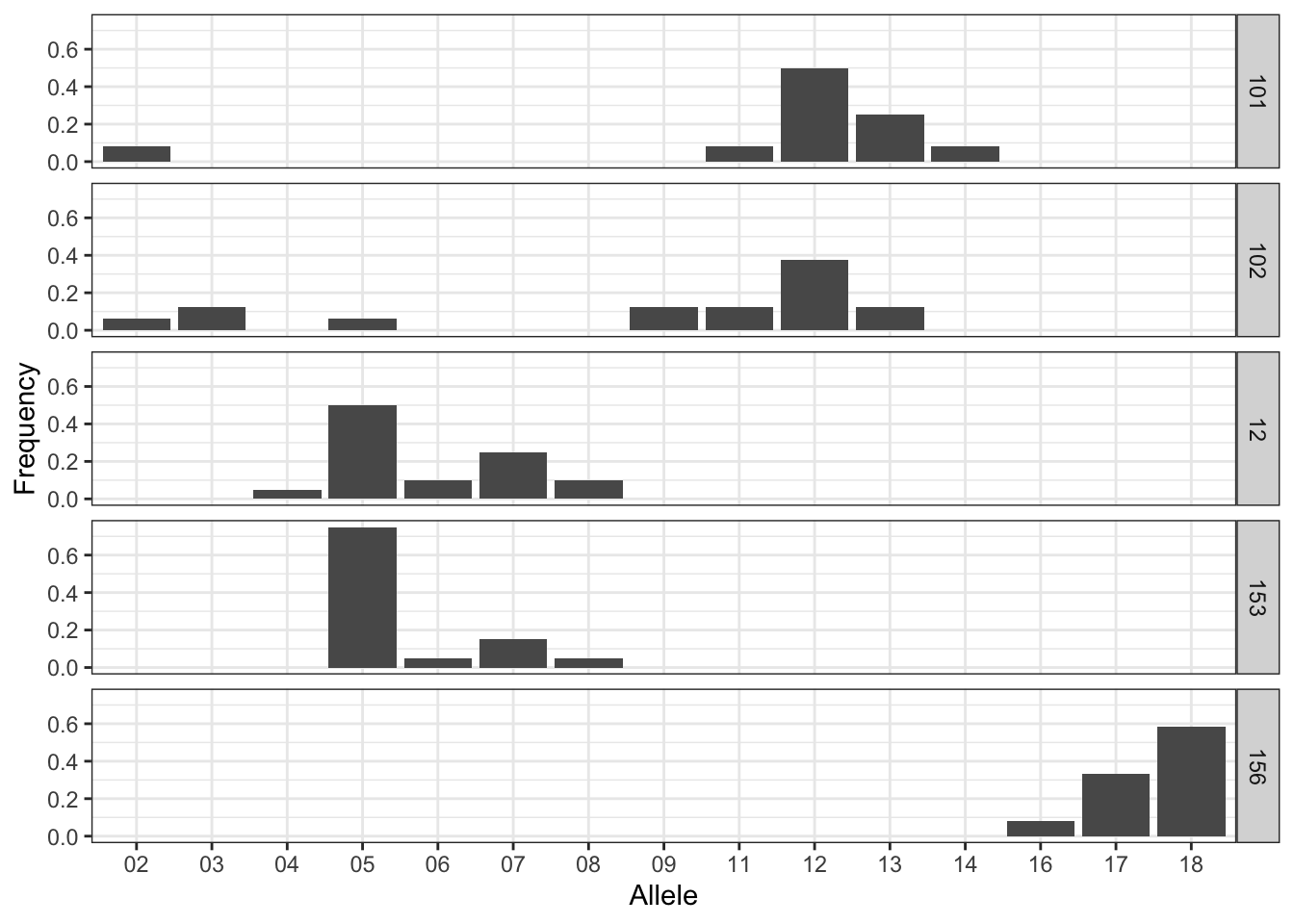

OK. Now, lets take a look at how we can make a random population. The make_population() function takes a frequency matrix and creates random individuals. Here is an example.

fake101 <- make_population( sim_freqs %>% filter(Stratum=="101"), N=100 )
Warning in make_loci(f, N, F): Your allele frequencies do not add to 1.0.  The
difference of 3.70074341541719e-17 will be partioned across all noted alleles
head(fake101)
  Population ID   AML  ATPS    EF    EN  LTRS  MP20   WNT   ZMP
1        101  1 11:11 02:09 01:01 03:03 02:02 12:13 01:01 01:01
2        101  2 08:11 02:02 01:01 01:03 02:02 12:12 01:01 01:01
3        101  3 11:11 02:02 01:02 01:01 02:02 13:13 01:01 01:01
4        101  4 08:11 02:04 01:01 01:03 02:02 12:13 01:01 01:01
5        101  5 11:11 02:09 02:02 03:03 01:02 12:14 01:01 01:01
6        101  6 08:11 02:02 01:02 01:03 02:02 11:12 01:01 01:01

The frequencies should be pretty close to the real ones. Compare the LTRS locus allele frequencies from the simualted data

frequencies( fake101,loci = "LTRS") 
  Locus Allele Frequency
1  LTRS     01      0.28
2  LTRS     02      0.72

and the real data

sim_freqs %>% filter(Locus=="LTRS", Stratum=="101")
  Stratum Locus Allele Frequency
1     101  LTRS     01 0.2777778
2     101  LTRS     02 0.7222222

Pretty close. So using this approach, we can make all kinds of allele random populations. You just need to figure out the allele frequency matrix and then pass that to the appropriate functions.